TecnoFisica: noviembre 2011

martes, 15 de noviembre de 2011

Formulas

La formula de la Fuerza es:

F = M * a (Fuerza es igual a la masa "M" por la aceleración "a")

Fuerza gravitatoria:

$\mathbf{F}_{21} = -G\frac{m_1m_2}{|\mathbf{r}_{21}|^2}\mathbf{e}_{21} = -G\frac{m_1m_2}{|\mathbf{r}_{21}|^3}\mathbf{r}_{21}$

Donde:

$\mathbf{F}_{21}$ es la fuerza que actúa sobre el cuerpo 2, ejercida por el cuerpo 1.

$G\,$ constante de la gravitación universal.

$\mathbf{r}_{21}=\mathbf r_2 -\mathbf r_1$ vector de posición relativo del cuerpo 2 respecto al cuerpo 1.

$\mathbf{e}_{21}$ es el vector unitario dirigido desde 1 hacía 2.

$m_1, m_2\,$ masas de los cuerpos 1 y 2.

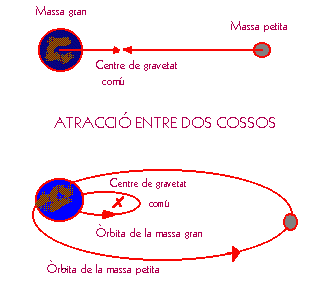
Cuando la masa de uno de los cuerpos es muy grande en comparación con la del otro (por ejemplo, si tiene dimensiones planetarias), la expresión anterior se transforma en otra más simple:

$\mathbf{F} = -m\left(G\frac{M}{R_0^2}\right) \hat{\mathbf{u}}_r = -mg\hat{\mathbf{u}}_r = m\mathbf{g}$

Fuerza entre cargas:

En mecánica newtoniana también es posible modelizar algunas fuerzas constantes en el tiempo como campos de fuerza. Por ejemplo la fuerza entre dos cargas eléctricas inmóviles, puede representarse adecuadamente mediante la ley de Coulomb:

$\mathbf{F}_{12} = -\kappa\frac{q_1q_2}{\|\mathbf{r}_{12}\|^3}\mathbf{r}_{12}$

Donde:

$\mathbf{F}_{12}$ es la fuerza ejercida por la carga 1 sobre la carga 2.

$\kappa\,$ una constante que dependerá del sistema de unidades para la carga.

$\mathbf{r}_{12}$ vector de posición de la carga 2 respecto a la carga 1.

$q_1, q_2\,$ valor de las cargas.

También los campos magnéticos estáticos y los debidos a cargas estáticas con distribuciones más complejas pueden resumirse en dos funciones vectoriales llamadas campo eléctrico y campo magnético tales que una partícula en movimiento respecto a las fuentes estáticas de dichos campos viene dada por la expresión de Lorentz:

$\mathbf{F} = q (\mathbf{E} + \mathbf{v} \times \mathbf{B}),$

Donde:

$\mathbf{E}$ es el campo eléctrico.

$\mathbf{B}$ es el campo magnético.

$\mathbf{v}$ es la velocidad de la partícula.

$q\,$ es la carga total de la partícula.

Fuerza centrípeta:

$\mathbf{F} = - \frac{m v^2}{r}\hat{\mathbf u}_r = - m \omega^2 \mathbf{r}$

m= masa
$r \,$ es el radio de la trayectoria circular (en general, el radio de curvatura).

el vector de posición.

el versor radial.

la velocidad angular.

Fuerza centrífuga:

En general, la fuerza centrífuga asociada a una partícula de masa $m\,$ en un sistema de referencia en rotación con una velocidad angular $\mathbf\omega\,$ y en una posición $\mathbf r\,$ respecto del eje de rotación se expresa:

$\mathbf F_\text{cf}= -m \boldsymbol\omega \times (\boldsymbol\omega \times \mathbf r)$

Por lo tanto, el módulo de esta fuerza se expresa:

$|\mathbf F_\text{cf}|= m\boldsymbol\omega^2 \mathbf r$

Fuerza de fricción

La fuerza de fricción se da a partir del contacto entre dos cuerpos. En realidad, éste efecto siempre está presente en el movimiento de un cuerpo debido a que siempre se desplaza haciendo contacto con otro (el aire en la mayoría de los casos); en algunos casos, éste efecto es muy pequeño y es una buena aproximación despreciar su valor, pero en otros, es necesario tomar en cuenta ésta fuerza, debido a que determina el valor del movimiento.

Fricción cinética

Cuando un cuerpo descansa sobre una superficie, podemos expresar la fuerza de contacto (por tercera ley del movimiento) en términos de sus componentes paralela y perpendicular a la superficie: la componente perpendicular es la fuerza normal N y la paralela a la superficie es la de fricción Ff. La dirección de Ff siempre es opuesta al movimiento relativo de las dos superficies.

El tipo de fricción que actúa cuando un cuerpo se desliza sobre una superficie es la fuerza de fricción cinética, Ffk (*). Ésta fuerza es proporcional a la normal: Ffk α N.

La constante de proporcionalidad para la relación anterior recibe el nombre de coneficiente de fricción cinética µk y su valor depende de la superficie: mientras mas lisa (como el lago congelado del ejemplo de la lección anterior) es la superficie, menor será el valor de la constante. Entonces, la fuerza de fricción cinética se define como:

Ffk = µk * N

Ésta es una ecuación escalar y válida solo para las magnitudes de las componentes de la fuerza de contacto.

La fuerza de fricción también puede actuar cuando no hay movimiento. En éste caso recibe el nombre de fuerza de fricción estática Ffs. Suponga que una persona empuja una caja sobre el piso tratando de moverla, pero no lo consigue, debido a que el piso ejerce una fuerza Ffs. Ésta fuerza también es proporcional a la normal y la constante de proporcionalidad se conoce como coeficiente de fricción estática µs. En algún punto, Ff es mayor que µs*N, que es cuando hay movimiento y Ff es Ffk = µk * N. Pero, mientras no exista movimiento, Ff es:

Ffs ≤ µs * N

Es decir, Ffs está entre 0 y (µs * N).

Fuerza gravitatoria o fuerza de gravedad

La gravedad, denominada también fuerza gravitatoria, fuerza de gravedad, interacción gravitatoria o gravitación, es la fuerza teórica de atracción que experimentan entre sí los objetos con masa.

Tiene relación con la fuerza que se conoce como peso. El peso, que es familiar a todos, es la fuerza de gravedad que ejerce la masa de la Tierra, respecto cualquier objeto que esté en su entorno, por ejemplo, la masa del cuerpo humano. Se aprovecha esta fuerza para medir la masa de los objetos con bastante precisión, por medio de básculas de pesas. La precisión alcanzada al pesar se debe a que la fuerza de gravedad que existe entre la tierra y los objetos de su superficie es similar en cualquier lugar que esté a la misma distancia del centro terrestre, aunque esta disminuirá proporcionalmente si se alejan, tanto de la pesa como del objeto a pesar.

En otros planetas o satélites, el peso de los objetos varía si la masa de los planetas o satélites es diferente (mayor o menor) a la masa de la Tierra.

Los efectos de la gravedad son siempre atractivos, y la fuerza resultante se calcula respecto del centro de gravedad de ambos objetos (en el caso de la Tierra, el centro de gravedad es su centro de masas, al igual que en la mayoría de los cuerpos celestes de características homogéneas).

La gravedad tiene un alcance teórico infinito, sin embargo, la fuerza es mayor si los objetos están cerca uno del otro, y mientras se van alejando dicha fuerza pierde intensidad. La pérdida de intensidad de esta fuerza es proporcional al cuadrado de la distancia que los separa. Por ejemplo, si se aleja un objeto de otro al doble de distancia, entonces la fuerza de gravedad será la cuarta parte.

La gravedad, en física, es una de las cuatro interacciones fundamentales. Origina la aceleración que experimenta un objeto en las cercanías de un objeto astronómico. También se denomina interacción gravitatoria o gravitación.

Por efecto de la gravedad tenemos la sensación de peso. Si estamos situados en las proximidades de un planeta, experimentamos una aceleración dirigida hacia la zona central de dicho planeta —si no estamos sometidos al efecto de otras fuerzas. En la superficie de la Tierra, la aceleración originada por la gravedad es 9.81 m/s2, aproximadamente.

Albert Einstein demostró que la gravedad no es una fuerza de atracción, sino una manifestación de la distorsión de la geometría del espacio-tiempo bajo la influencia de los objetos que lo ocupan.

Albert Einstein demostró que puede representarse como campo tensorial de fuerzas ficticias: «Dicha fuerza es una ilusión, un efecto de la geometría del espacio-tiempo. La Tierra deforma el espacio-tiempo de nuestro entorno, de manera que el propio espacio nos empuja hacia el suelo».

La gravedad posee características atractivas, mientras que la denominada energía oscura tendría características de fuerza gravitacional repulsiva, causando la acelerada expansión del Universo.

Fuerza centrífuga

La fuerza centrífuga es una fuerza ficticia que aparece cuando se describe el movimiento de un cuerpo en un sistema de referencia en rotación, o equivalentemente la fuerza aparente que percibe un observador no inercial que se encuentra en un sistema de referencia giratorio.

El calificativo de "centrífuga" significa que "huye del centro". En efecto, un observador no inercial situado sobre una plataforma giratoria siente que existe una «fuerza» que actúa sobre él, que le impide permanecer en reposo sobre la plataforma a menos que él mismo realice otra fuerza dirigida hacia el eje de rotación. Así, aparentemente, la fuerza centrífuga tiende a alejar los objetos del eje de rotación.

$\mathbf F_\text{cf}= -m \boldsymbol\omega \times (\boldsymbol\omega \times \mathbf r)$

Por lo tanto, el módulo de esta fuerza se expresa:

$|\mathbf F_\text{cf}|= m\boldsymbol\omega^2 \mathbf r$

La aceleración centrífuga es aquella que adquieren los cuerpos por causa del "efecto fuerza centrifuga".

Antes que nada cabe aclarar que la fuerza centrífuga es una fuerza de inercia. Como toda fuerza de inercia resulta de describir el movimiento de una partícula o sistema de partículas desde un sistema de referencia no inercial.

Fuerza centrípeta

La fuerza centrípeta es el componente de fuerza, dirigida hacia el centro de curvatura de la trayectoria, que actúa sobre un objeto en movimiento sobre una trayectoria curvilínea.

El término «centrípeta» proviene de las palabras latinas centrum, «centro» y petere, «dirigirse hacia», y puede ser obtenida a partir de las leyes de Newton. La fuerza centrípeta siempre actúa en forma perpendicular a la dirección del movimiento del cuerpo sobre el cual se aplica. En el caso de un objeto que se mueve en trayectoria circular con velocidad cambiante, la fuerza neta sobre el cuerpo puede ser descompuesta en un componente perpendicular que cambia la dirección del movimiento y uno tangencial, paralelo a la velocidad, que modifica el módulo de la velocidad.

Los objetos con movimiento rectilíneo uniforme tienen una velocidad constante; pero un objeto que se mueva sobre una trayectoria circular con velocidad constante experimenta continuamente un cambio en la dirección de su movimiento, esto es, en la dirección de la velocidad. Puesto que la velocidad cambia, existe una aceleración. La magnitud de este cambio de dirección de la velocidad por unidad de tiempo es la aceleración centrípeta, representada por un vector dirigido hacia el centro de la circunferencia dado por

$\mathbf{a} = -\frac{v^2}{r} \left (\frac{\mathbf{r}}{r}\right ) = -\frac{v^2}{r}\hat{\mathbf u}_r = - \omega^2 \mathbf{r}$

Donde:

$\mathbf{a} \,$ es la aceleración centrípeta.

$v \,$ es el módulo de la velocidad.

$r \,$ es el radio de la trayectoria circular (en general, el radio de curvatura).

$\mathbf{r} \,$ el vector de posición.

$\mathbf{u}_r \,$ el versor radial.

$\omega \,$ la velocidad angular.

Según la segunda ley de Newton, para que se produzca una aceleración debe actuar una fuerza en la dirección de esa aceleración. Así, si consideramos una partícula de masa

en movimiento circular uniforme, estará sometida a una fuerza centrípeta dada por:

$\mathbf{F} = - \frac{m v^2}{r}\hat{\mathbf u}_r = - m \omega^2 \mathbf{r}$

Fuerza eléctrica

Entre dos o más cargas aparece una fuerza denominada fuerza eléctrica cuyo módulo depende de el valor de las cargas y de la distancia que las separa, mientras que su signo depende del signo de cada carga. Las cargas del mismo signo se repelen entre sí, mientras que las de distinto signo se atraen.

La fuerza entre dos cargas se calcula como:

q1, q2 = Valor de las cargas 1 y 2
d = Distancia de separación entre las cargas
Fe = Fuerza eléctrica

La fuerza es una magnitud vectorial, por lo tanto además de determinar el módulo se deben determinar dirección y sentido.

Dirección de la fuerza eléctrica

Si se trata únicamente de dos cargas, la dirección de la fuerza es colineal a la recta que une ambas cargas.

Sentido de la fuerza eléctrica

El sentido de la fuerza actuante entre dos cargas es de repulsión si ambas cargas son del mismo signo y de atracción si las cargas son de signo contrario.

Fuerzas originadas por varias cargas sobre otra

Si se tienen varias cargas y se quiere hallar la fuerza resultante sobre una de ellas, lo que se debe hacer es plantear cada fuerza sobre la carga (una por cada una de las otras cargas). Luego se tienen todas las fuerzas actuantes sobre esta carga y se hace la composición de fuerzas, con lo que se obtiene un vector resultante.